Manual On Stepwise Regression
Mar 24, 2017 Stepwise Regression. This analysis performs an automated stepwise regression on genetic data, which builds a model by successively adding or removing variables using an F-test to determine their significance. Example 64.1 Stepwise Regression. Krall, Uthoff, and Harley (1975) analyzed data from a study on multiple myeloma in which researchers treated 65 patients.
Machine learning Machine learning is becoming widespread among data scientist and is deployed in hundreds of products you use daily. One of the first ML application was spam filter. Following are other application of Machine Learning-. Identification of unwanted spam messages in email. Segmentation of customer behavior for targeted advertising. Reduction of fraudulent credit card transactions.
Optimization of energy use in home and office building. Facial recognition Before you start to implement machine learning algorithm, let's study the difference between supervised learning and unsupervised learning. This tutorial introduces some fundamental concepts in data science. In this tutorial, you will learn. Supervised learning In supervised learning, the training data you feed to the algorithm includes a label. Classification is probably the most used supervised learning technique.
One of the first classification task researchers tackled was the spam filter. The objective of the learning is to predict whether an email is classified as spam or ham (good email). The machine, after the training step, can detect the class of email. Regressions are commonly used in the machine learning field to predict continuous value. Regression task can predict the value of a dependent variable based on a set of independent variables (also called predictors or regressors).
For instance, linear regressions can predict a stock price, weather forecast, sales and so on. Here is the list of some fundamental supervised learning algorithms. Linear regression. Logistic regression. Nearest Neighbors. Support Vector Machine (SVM).
Decision trees and Random Forest. Neural Networks Unsupervised learning In unsupervised learning, the training data is unlabeled. The system tries to learn without a reference. Below is a list of unsupervised learning algorithms. K-mean. Hierarchical Cluster Analysis. Expectation Maximization.
Visualization and dimensionality reduction. Principal Component Analysis. Kernel PCA. Locally-Linear Embedding Simple Linear regression Linear regression answers a simple question: Can you measure an exact relationship between one target variables and a set of predictors? The simplest of probabilistic models is the straight line model: where.
y = Dependent variable. x = Independent variable.
= random error component. = intercept. = Coefficient of x Consider the following plot: The equation is is the intercept. If x equals to 0, y will be equal to the intercept, 4.77. Is the slope of the line. It tells in which proportion y varies when x varies. To estimate the optimal values of and, you use a method called Ordinary Least Squares (OLS).
This method tries to find the parameters that minimize the sum of the squared errors, that is the vertical distance between the predicted y values and the actual y values. The difference is known as the error term. Before you estimate the model, you can determine whether a linear relationship between y and x is plausible by plotting a scatterplot. Scatterplot We will use a very simple dataset to explain the concept of simple linear regression. We will import the Average Heights and weights for American Women. The dataset contains 15 observations. You want to measure whether Heights are positively correlated with weights.
Library(ggplot2) path. The scatterplot suggests a general tendency for y to increase as x increases. In the next step, you will measure by how much increases for each additional.

Least Squares Estimates In a simple OLS regression, the computation of and is straightforward. The goal is not to show the derivation in this tutorial. You will only write the formula. You want to estimate: The goal of the OLS regression is to minimize the following equation: where is the actual value and is the predicted value. The solution for is Note that means the average value of x The solution for is In R, you can use the covand varfunction to estimate and you can use the mean function to estimate beta.
The dependent variable y is now a function of k independent variables. The value of the coefficient determines the contribution of the independent variable. We briefly introduce the assumption we made about the random error of the OLS:. Mean equal to 0. Variance equal to. Normal distribution.
Random errors are independent (in a probabilistic sense) You need to solve for, the vector of regression coefficients that minimise the sum of the squared errors between the predicted and actual y values. The closed-form solution is: with:.
indicates the transpose of the matrix X. indicates the invertible matrix We use the mtcars dataset. You are already familiar with the dataset. Our goal is to predict the mile per gallon over a set of features.
Continuous variables For now, you will only use the continuous variables and put aside categorical features. The variable am is a binary variable taking the value of 1 if the transmission is manual and 0 for automatic cars; vs is also a binary variable. Library(dplyr) df% select(-c(am, vs, cyl, gear, carb)) glimpse(df) Output: ## Observations: 32 ## Variables: 6 ## $ mpg 21.0, 21.0, 22.8, 21.4, 18.7, 18.1, 14.3, 24.4, 22.8, 19. ## $ disp 160.0, 160.0, 108.0, 258.0, 360.0, 225.0, 360.0, 146.7, 1. ## $ hp 110, 110, 93, 110, 175, 105, 245, 62, 95, 123, 123, 180.
## $ drat 3.90, 3.90, 3.85, 3.08, 3.15, 2.76, 3.21, 3.69, 3.92, 3.9. ## $ wt 2.620, 2.875, 2.320, 3.215, 3.440, 3.460, 3.570, 3.190, 3. ## $ qsec 16.46, 17.02, 18.61, 19.44, 17.02, 20.22, 15.84, 20.00, 2. You can use the lm function to compute the parameters. The basic syntax of this function is: lm(formula, data, subset) Arguments: -formula: The equation you want to estimate -data: The dataset used -subset: Estimate the model on a subset of the dataset Remember an equation is of the following form in R. The symbol = is replaced by.
Each x is replaced by the variable name. If you want to drop the constant, add -1 at the end of the formula Example: You want to estimate the weight of individuals based on their height and revenue. The equation is The equation in R is written as follow: y X1+ X2+.+Xn # With intercept So for our example. Weigh height + revenue Your objective is to estimate the mile per gallon based on a set of variables. The equation to estimate is: You will estimate your first linear regression and store the result in the fit object.
Model t ) ## (Intercept) 16.5333 1.508 0.14362 ## disp 0.00872 0.01119 0.779 0.44281 ## hp -0.02060 0.01528 -1.348 0.18936 ## drat 2.01578 1.30946 1.539 0.13579 ## wt -4.38546 1.24343 -3.527 0.00158. ## qsec 0.64015 0.45934 1.394 0.17523 ## - ## Signif. Codes: 0 '.' 0.001 '.' 0.01 '.'
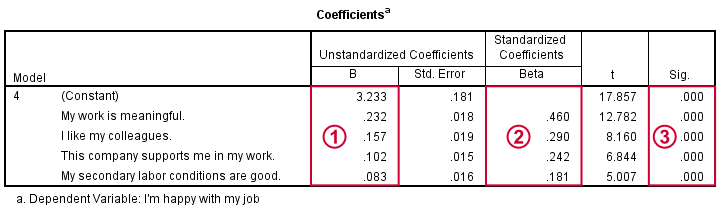
0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 2.558 on 26 degrees of freedom ## Multiple R-squared: 0.8489, Adjusted R-squared: 0.8199 ## F-statistic: 29.22 on 5 and 26 DF, p-value: 6.892e-10 Inference from the above table output. The above table proves that there is a strong negative relationship between wt and mileage and positive relationship with drat. Only the variable wt has a statistical impact on mpg. Remember, to test a hypothesis in statistic, we use:. H0: No statistical impact.
H3: The predictor has a meaningful impact on y. If the p value is lower than 0.05, it indicates the variable is statistically significant. Adjusted R-squared: Variance explained by the model.
In your model, the model explained 82 percent of the variance of y. R squared is always between 0 and 1.
The higher the better You can run the ANOVA test to estimate the effect of each feature on the variances with the anova function. Anova(fit) Output: ## Analysis of Variance Table ## ## Response: mpg ## Df Sum Sq Mean Sq F value Pr(F) ## disp 1 808.89 808.89 123.6185 2.23e-11. ## hp 1 33.67 33.67 5.1449 0.031854.
## drat 1 30.15 30.15 4.6073 0.041340. ## wt 1 70.51 70. 0.002933.
## qsec 1 12.71 12.71 1.9422 0.175233 ## Residuals 26 170.13 6.54 ## - ## Signif. Codes: 0 '.' 0.001 '.' 0.01 '.' 0.05 '.' 0.1 ' ' 1 A more conventional way to estimate the model performance is to display the residual against different measures.
You can use the plot function to show four graphs: - Residuals vs Fitted values - Normal Q-Q plot: Theoretical Quartile vs Standardized residuals - Scale-Location: Fitted values vs Square roots of the standardised residuals - Residuals vs Leverage: Leverage vs Standardized residuals You add the code par(mfrow=c(2,2)) before plot(fit). If you don't add this line of code, R prompts you to hit the enter command to display the next graph. Par(mfrow=(2,2)) Code Explanation.
Manual On Stepwise Regression In R
(mfrow=c(2,2)): return a window with the four graphs side by side. The first 2 adds the number of rows.
The second 2 adds the number of columns. If you write (mfrow=c(3,2)): you will create a 3 rows 2 columns window plot(fit) Output: The lm formula returns a list containing a lot of useful information.
You can access them with the fit object you have created, followed by the $ sign and the information you want to extract. coefficients: `fit$coefficients` - residuals: `fit$residuals` - fitted value: `fit$fitted.values` Factors regression In the last model estimation, you regress mpg on continuous variables only. It is straightforward to add factor variables to the model. You add the variable am to your model. It is important to be sure the variable is a factor level and not continuous. Df% mutate(cyl = factor(cyl), vs = factor(vs), am = factor(am), gear = factor(gear), carb = factor(carb)) summary(lm(model, df)) Output: ## ## Call: ## lm(formula = model, data = df) ## ## Residuals: ## Min 1Q Median 3Q Max ## -3.5087 -1.3584 -0.0948 0.7745 4.6251 ## ## Coefficients: ## Estimate Std. Error t value Pr( t ) ## (Intercept) 23.8792 1.190 0.2525 ## cyl6 -2.64870 3.04089 -0.871 0.3975 ## cyl8 -0.33616 7.15954 -0.047 0.9632 ## disp 0.03555 0.03190 1.114 0.2827 ## hp -0.07051 0.03943 -1.788 0.0939.
## drat 1.18283 2.48348 0.476 0.6407 ## wt -4.52978 2.53875 -1.784 0.0946. ## qsec 0.36784 0.93540 0.393 0.6997 ## vs1 1.93085 2.87126 0.672 0.5115 ## am1 1.21212 3.21355 0.377 0.7113 ## gear4 1.11435 3.79952 0.293 0.7733 ## gear5 2.52840 3.73636 0.677 0.5089 ## carb2 -0.97935 2.31797 -0.423 0.6787 ## carb3 2.99964 4.29355 0.699 0.4955 ## carb4 1.09142 4.44962 0.245 0.8096 ## carb6 4.47757 6.38406 0.701 0.4938 ## carb8 7.25041 8.36057 0.867 0.3995 ## - ## Signif.
Codes: 0 '.' 0.001 '.' 0.01 '.' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 2.833 on 15 degrees of freedom ## Multiple R-squared: 0.8931, Adjusted R-squared: 0.779 ## F-statistic: 7.83 on 16 and 15 DF, p-value: 0.000124 R uses the first factor level as a base group. You need to compare the coefficients of the other group against the base group.
Stepwise regression The last part of this tutorial deals with the stepwise regression algorithm. The purpose of this algorithm is to add and remove potential candidates in the models and keep those who have a significant impact on the dependent variable. This algorithm is meaningful when the dataset contains a large list of predictors. You don't need to manually add and remove the independent variables. The stepwise regression is built to select the best candidates to fit the model. Let's see in action how it works. You use the mtcars dataset with the continuous variables only for pedagogical illustration.
Before you begin analysis, its good to establish variations between the data with a correlation matrix. The GGally library is an extension of ggplot2. The library includes different functions to show summary statistics such as correlation and distribution of all the variables in a matrix. We will use the ggscatmat function, but you can refer to the for more information about the GGally library. The basic syntax for ggscatmat is: ggscatmat(df, columns = 1:ncol(df), corMethod = 'pearson') arguments: -df: A matrix of continuous variables -columns: Pick up the columns to use in the function. By default, all columns are used -corMethod: Define the function to compute the correlation between variable.
By default, the algorithm uses the Pearson formula You display the correlation for all your variables and decides which one will be the best candidates for the first step of the stepwise regression. There are some strong correlations between your variables and the dependent variable, mpg. Library(GGally) df% select(-c(am, vs, cyl, gear, carb)) ggscatmat(df, columns = 1: ncol(df)) Output: Stepwise regression Variables selection is an important part to fit a model. The stepwise regression will perform the searching process automatically.
To estimate how many possible choices there are in the dataset, you compute with k is the number of predictors. The amount of possibilities grows bigger with the number of independent variables. That's why you need to have an automatic search. You need to install the olsrr package from CRAN.
Manual Stepwise Regression
The package is not available yet in Anaconda. Hence, you install it directly from the command line: install.packages('olsrr') You can plot all the subsets of possibilities with the fit criteria (i.e. R-square, Adjusted R-square, Bayesian criteria). The model with the lowest AIC criteria will be the final model. Library(olsrr) model t ) ## (Intercept) 37.22727 1.59879 23.285.
In, stepwise regression is a method of fitting in which the choice of predictive variables is carried out by an automatic procedure. In each step, a variable is considered for addition to or subtraction from the set of based on some prespecified criterion. Usually, this takes the form of a sequence of or, but other techniques are possible, such as,.
The frequent practice of fitting the final selected model followed by reporting estimates and confidence intervals without adjusting them to take the model building process into account has led to calls to stop using stepwise model building altogether or to at least make sure model uncertainty is correctly reflected. In this example from engineering, necessity and sufficiency are usually determined. For additional consideration, when planning an, or scientific to collect for this, one must keep in mind the number of, P, to and adjust the accordingly.
For K, P = 1 (Start) + K (Stage I) + ( K 2 − K)/2 (Stage II) + 3 K (Stage III) = 0.5 K 2 + 3.5 K + 1. Contents. Main approaches The main approaches are:. Forward selection, which involves starting with no variables in the model, testing the addition of each variable using a chosen model fit criterion, adding the variable (if any) whose inclusion gives the most statistically significant improvement of the fit, and repeating this process until none improves the model to a statistically significant extent. Backward elimination, which involves starting with all candidate variables, testing the deletion of each variable using a chosen model fit criterion, deleting the variable (if any) whose loss gives the most statistically insignificant deterioration of the model fit, and repeating this process until no further variables can be deleted without a statistically significant loss of fit. Bidirectional elimination, a combination of the above, testing at each step for variables to be included or excluded.
Selection criterion. Main article: A way to test for errors in models created by step-wise regression, is to not rely on the model's F-statistic, significance, or multiple R, but instead assess the model against a set of data that was not used to create the model. This is often done by building a model based on a sample of the dataset available (e.g., 70%) – the “” – and use the remainder of the dataset (e.g., 30%) as a to assess the accuracy of the model. Accuracy is then often measured as the actual standard error (SE), MAPE, or mean error between the predicted value and the actual value in the hold-out sample. This method is particularly valuable when data are collected in different settings (e.g., different times, social vs. Solitary situations) or when models are assumed to be generalizable. Criticism Stepwise regression procedures are used in, but are controversial.
Several points of criticism have been made. The tests themselves are biased, since they are based on the same data. Wilkinson and Dallal (1981) computed percentage points of the multiple correlation coefficient by simulation and showed that a final regression obtained by forward selection, said by the F-procedure to be significant at 0.1%, was in fact only significant at 5%.
When estimating the, the number of the candidate independent variables from the best fit selected may be smaller than the total number of final model variables, causing the fit to appear better than it is when adjusting the r 2 value for the number of degrees of freedom. It is important to consider how many degrees of freedom have been used in the entire model, not just count the number of independent variables in the resulting fit. Models that are created may be over-simplifications of the real models of the data. Such criticisms, based upon limitations of the relationship between a model and procedure and data set used to fit it, are usually addressed by the model on an independent data set, as in the. Critics regard the procedure as a paradigmatic example of, intense computation often being an inadequate substitute for subject area expertise.
Additionally, the results of stepwise regression are often used incorrectly without adjusting them for the occurrence of model selection. Especially the practice of fitting the final selected model as if no model selection had taken place and reporting of estimates and confidence intervals as if least-squares theory were valid for them, has been described as a scandal. Widespread incorrect usage and the availability of alternatives such as, leaving all variables in the model, or using expert judgement to identify relevant variables have led to calls to totally avoid stepwise model selection. See also. References. Efroymson,M.
(1960) 'Multiple regression analysis,' Mathematical Methods for Digital Computers, Ralston A. S., (eds.), Wiley, New York.
Hocking, R. (1976) 'The Analysis and Selection of Variables in Linear Regression,' Biometrics, 32. And Smith, H. (1981) Applied Regression Analysis, 2d Edition, New York: John Wiley & Sons, Inc. (1989) SAS/STAT User's Guide, Version 6, Fourth Edition, Volume 2, Cary, NC: Inc.
And Cassell, D. (2007) 'Stopping stepwise: Why stepwise and similar selection methods are bad, and what you should use,' NESUG 2007. Harrell, F. (2001) 'Regression modeling strategies: With applications to linear models, logistic regression, and survival analysis,' Springer-Verlag, New York. ^ Chatfield, C. (1995) 'Model uncertainty, data mining and statistical inference,' J. A 158, Part 3, pp.
And Tibshirani, R. (1998) 'An introduction to the bootstrap,' Chapman & Hall/CRC.
from a at. Efroymson, MA (1960) 'Multiple regression analysis.' In Ralston, A. And Wilf, HS, editors, Mathematical Methods for Digital Computers.
Foster, Dean P., & George, Edward I. The Risk Inflation Criterion for Multiple Regression., 22(4). 1947–1975.:. Donoho, David L., & Johnstone, Jain M. Ideal spatial adaptation by wavelet shrinkage., 81(3):425–455.:.
Mark, Jonathan, & Goldberg, Michael A. Multiple regression analysis and mass assessment: A review of the issues. The Appraisal Journal, Jan., 89–109.
Mayers, J.H., & Forgy, E.W. The Development of numerical credit evaluation systems.
Forward Stepwise Regression
Journal of the American Statistical Association, 58(303; Sept), 799–806. Rencher, A. C., & Pun, F. Inflation of R² in Best Subset Regression. Technometrics, 22, 49–54.
Copas, J.B. Regression, prediction and shrinkage. Series B, 45, 311–354. Wilkinson, L., & Dallal, G.E.
Tests of significance in forward selection regression with an F-to enter stopping rule. Technometrics, 23, 377–380. Hurvich, C. The impact of model selection on inference in linear regression.
American Statistician 44: 214–217. Roecker, Ellen B. Prediction error and its estimation for subset—selected models. Technometrics, 33, 459–468.